网站数据分析：如何衡量数据的离散程度

发布时间：2013-01-27 20:21:39作者：知识屋

　　我们通常使用均值、中位数、众数等统计量来反映数据的集中趋势，但这些统计量无法完全反应数据的特征，即使均值相等的数据集也存在无限种分布的可能，所以需要结合数据的离散程度。常用的可以反映数据离散程度的统计量如下：

　　极差(Range)

　　极差也叫全距，指数据集中的最大值与最小值之差：

　　极差计算比较简单，能从一定程度上反映数据集的离散情况，但因为最大值和最小值都取的是极端，而没有考虑中间其他数据项，因此往往会受异常点的影响不能真实反映数据的离散情况。

　　四分位距(interquartile range，IQR)

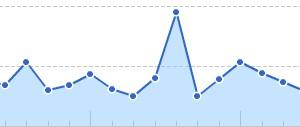
　　我们通常使用箱形图来表现一个数据集的分布特征：

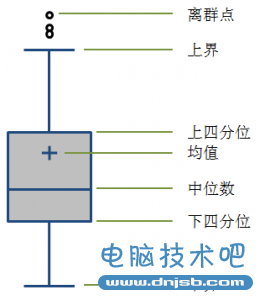
　　一般中间矩形箱的上下两边分别为数据集的上四分位数(75%，Q3)和下四分位数(25%，Q1)，中间的横线代表数据集的中位数(50%，Media，Q2)，四分位距是使用Q3减去Q1计算得到：

　　如果将数据集升序排列，即处于数据集3/4位置的数值减去1/4位置的数值。四分位距规避了数据集中存在异常大或者异常小的数值影响极差对离散程度的判断，但四分位距还是单纯的两个数值相减，并没有考虑其他数值的情况，所以也无法比较完整地表现数据集的整体离散情况。

　　方差(Variance)

　　方差使用均值作为参照系，考虑了数据集中所有数值相对均值的偏离情况，并使用平方的方式进行求和取平均，避免正负数的相互抵消：

　　方差是最常用的衡量数据离散情况的统计量。

　　标准差(Standard Deviation)

　　方差得到的数值偏差均值取平方后的算术平均数，为了能够得到一个跟数据集中的数值同样数量级的统计量，于是就有了标准差，标准差就是对方差取开方后得到的：

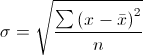
　　基于均值和标准差就可以大致明确数据集的中心及数值在中心周围的波动情况，也可以计算正态总体的置信区间等统计量。

　　平均差(Mean Deviation)

　　方差用取平方的方式消除数值偏差的正负，平均差用绝对值的方式消除偏差的正负性。平均差可以用均值作为参考系，也可以用中位数，这里使用均值：

　　平均差相对标准差而言，更不易受极端值的影响，因为标准差是通过方差的平方计算而来的，但是平均差用的是绝对值，其实是一个逻辑判断的过程而并非直接计算的过程，所以标准差的计算过程更加简单直接。

　　变异系数(Coefficient of Variation，CV)

　　上面介绍的方差、标准差和平均差等都是数值的绝对量，无法规避数值度量单位的影响，所以这些统计量往往需要结合均值、中位数才能有效评定数据集的离散情况。比如同样是标准差是10的数据集，对于一个数值量级较大的数据集来说可能反映的波动是较小的，但是对于数值量级较小的数据集来说波动也可能是巨大的。

　　变异系数就是为了修正这个弊端，使用标准差除以均值得到的一个相对量来反映数据集的变异情况或者离散程度：

　　变异系数的优势就在于作为一个无量纲量，可以比较度量单位不同的数据集之间的离散程度的差异;缺陷也是明显的，就是无法反应真实的绝对数值水平，同时对于均值是0的数据集无能为力。

　　其实这篇文章只是对基础的统计知识的整理，可以从很多资料里面找到，很多统计学的书里面都是在“统计描述”章节中介绍这些基础的统计量，跟均值、中位数、众数等一起罗列，很少通过统计量的具体应用进行分类，而国外的一些书对知识点的介绍更多的是从实际应用的角度出发的，这里推荐《深入浅出统计学》这本书，虽然介绍的都是基础的统计知识，但可读性比较强，通俗易通，相比国内的一些统计学教程，更容易在大脑中建立起有效的知识索引，在具体应用中能够更加得心应手。

（免责声明：文章内容如涉及作品内容、版权和其它问题，请及时与我们联系，我们将在第一时间删除内容，文章内容仅供参考）