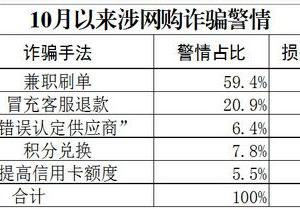
椭圆曲线密码体制与电子政务(图)

一 、概述       随着政府部门和行业对网络环境和网络资源依赖程度的增强,涉及国家安全和社会公共安全的所有重大问题都在网络上表现出来.在无纸化的电子政务中,特别是在公文流转中,如何保护电子化公文与传统方式一样安全可靠,是人们关注的焦点,也是电子政务全面应用的关键问题之一.目前,学术界和有关厂商在经过多年努力后,初步形成了一套解决方案,即被国外广泛应用的公开密钥基础设施(Public Key Infrastructure,PKI).PKI利用密码学理论对要传输的数字信息进行加密和签名,保证信息传输的机密性、真实性、完整性和不可否认性.         密码体制分为对称密码体制和非对称密码体制.非对称密码体制是指在加密过程中,密钥被分为一对.这对密钥中的任何一个密钥都可以作为公开密钥通过非保密方式向他人公开,而另一把作为私有密钥加以保存.这对密钥具有这样一个特点:当知道密钥对中的一个密钥时,要检测出另一个密钥,在计算上是不可能的.公开密钥用来对信息进行加密,则私有密钥用来对信息进行解密,反之亦然.在这个系统中,每个通信实体都有一个加密密钥和一个紧密相关的解密密钥.通信的双方只要知道对方的公钥,就可以进行安全的通信.         根据公钥密码体制基于的数学难题,有三类系统目前认为是安全的:大数分解系统,代表为RSA；离散对数系统,代表为DSA；椭圆曲线离散对数系统ECC.在这三个系统中,椭圆曲线离散对数密码体制用较短的密钥而得到较高的安全,各种参数比较如表1所示:     表1　三种公钥密码体制的参数比较   系统参数(比特) 公开密钥(比特) 私有密钥(比特) RSA      N/a      1088      2048 DSA      2208      1024      160 ECC      481       161      160         　         可见,在相当安全强度下,ECC具有很大的优越性,这些优越性在实现上意味着较高的速度,较低的计算消耗和代码量的减少.     二 椭圆曲线公钥密码体制   1、椭圆曲线的定义       射影平面P_k²上的齐次表达式          E: Y²Z+a₁XYZ+a₃YZ²=X³+a₂X²Z+a₄XZ²+a₆Z³称为Weirstrass等式.其中a₁,a₂,a₃,a₄,a₆∈Fq,Fq为有限域.         设:  F(X,Y,Z)= Y²Z+a₁XYZ+a₃YZ²-X³-a₂X²Z-a₄XZ²-a₆Z³,称F(X,Y,Z)为Weistrass多项式.当在任意点P成立,则椭圆曲线称为光滑的或非奇异的.若E是定义在有限域Fq上的椭圆曲线且其q=p^m(p为素数),这样的p称为有限域Fq的特征值.E中恰好有一个Z坐标为0的点(0,1,0),我们称它为椭圆曲线的无穷远点,用O表示.椭圆曲线上有理点的个数称为该椭圆曲线的阶,若亦#E(Fq)表示椭圆曲线的阶,则由#E(Fq)=q+1-t(其中t<＝2 ).即Hasse定理.         如果椭圆曲线E定义在域Fq上,其特征值不等于2和3 ,则E的Weirstrass等式可以简化,做变换: ,进而Weirstrass等式变换为Y²=X³+aX+b,其中a,b∈Fq,判别式Δ=4a³+27b²≠0此式为椭圆曲线的一般形式.若令x=X/Z,y=Y/Z,则等式变为 y³+a₁xy+a₃y=x³+a₂x²+a₄x+a₆   2、椭圆曲线上的加法运算       运算法则：任意取椭圆曲线上两点P、Q （若P、Q两点重合，则做P点的切线）做直线交于椭圆曲线的另一点R’，过R’做y轴的平行线交于R。则P+Q=R。（如图1） 
   

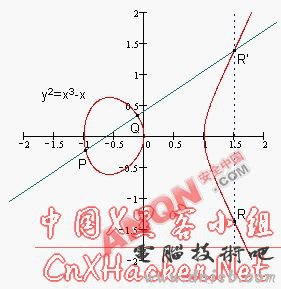
        图1 椭圆曲线上加法运算意义          根据这个法则，可以知道椭圆曲线无穷远点O与椭圆曲线上一点P的连线交于P’，过P’作y轴的平行线交于P，所以有 无穷远点 O+ P = P 。设P(x,y),则-P=P(x,-y).        对于一般的椭圆曲线方程y²+a₁xy+a₃y=x³+a₂x²+a₄x+a_6, 设点P(x₁,y₁)，Q(x₂,y₂)的和R(x₄,y₄)的坐标。R(x₄,y₄)的计算公式如下:  

       x₄=k²+ka₁+a₂+x₁+x₂;
       y₄=k(x₁-x₄)-y₁-a₁x₄-a₃;

        其中k= (y₁-y₂)/(x₁-x₂)     当P≠Q时             k=(3x₂+2a₂x+a₄ -a₁y) /(2y+a₁x+a₃) 当P=Q时         对于椭圆曲线方程Y²=X³+aX+b,上述的公式变为:

  x₄=θ²- x₁-x₂;   y₄=θ(x₁-x₃)-y₁

      其中θ=(y₁-y₂)/(x₁-x₂)     当P≠Q时;             θ=(3x₁²-a)/2y₁         当P=Q时         由上述运算公式,可以给出点积mP的运算,即mP=P+P+…+P,共m个P相加,这里m∈N.具体算法为:设m的二进制表示为 m=(m_n-1m_n-2…m₁m₀)，其中m_n-1=1,Q=P,从左到右依次计算:for(I=n-2 to 0)         {Q=2Q;if(m_i==1) Q=Q+P}         则Q=mP.   3、椭圆曲线的离散对数问题       简单地说,离散对数问题就是乘方过程的求”逆”,这个问题可以由各种不同的代数结构构成,最常见的类型有:

（1）有限域上的离散对数问题DLP:给定有限域Fq和元素g,h∈Fq,寻找一个整数d使在Fq中g^d=h;

（2）椭圆曲线离散对数问题ECDLP:给定定义于有限域Fq上的椭圆曲线E和E上的两点P,Q∈E(Fq),寻找一整数d使在E中有dP=Q。

        第二个问题比第一个问题更难解决,其根本原因是DLP(有限域)的代数       对象由两个基本运算构成:域元素的加法和乘法;而ECDLP(有限域上的椭圆曲线)的代数对象仅由一个基本运算构成:椭圆曲线上点的加法.DLP中的附加结构亚指数时间的索引计算方法求解DLP可行,而椭圆曲线没有类似的附加结构,因此不能用索引计算的方法求解ECDLP(除了特殊的一类椭圆曲线).椭圆曲线离散对数问题是构造椭圆曲线密码体制的数学基础.     三、椭圆曲线在电子政务中的安全应用         在实现无纸化的电子政务构成中,公文的流转通过网上实现,由于网络不提供安全保证,为了保证公文流转的安全性,可运用各种信息安全的技术,如:加密技术,密钥管理技术,数字签名技术等来满足信息安全的所有目标,即:   有效性　确保公文在确定的时刻确定的地点是有效的。 机密性　网络上没有绝对安全的通道,要预防信息的非法保存和泄漏.通过数据加密可以保证数据的机密性. 身份认证性　保证对方属于所声称的实体,通过数字签名来实现. 数据完整性　防止传递过程中信息丢失和重复.保证信息内容不被修改,入侵者 不可能用假信息代替合法的信息,通过数字签名来实现.         不可抵赖性　发送者不可能事后否认他发送过的信息,信息的接收方可以向中立的第三方CA机构证实所指的发送者确实发送了信息.通过数字签名来实现.          根据椭圆曲线密码体制的特点,以上几点都可以通过椭圆曲线密码体制用软件来实现.实现椭圆曲线的主要运算有:大数的点加,点积,平方剩余判断,明文消息编码为椭圆曲线上的点,模逆等.参考文献[3-5]给出了具体的算法和理论证明.   1、椭圆曲线参数的选择       在SECI及IEEE P1363ECC^[1]工作草案中,所定义的二进制域上椭圆曲线用到六个参量：  T=(p,a,b,G,n,h)。
      （p 、a 、b 用来确定一条椭圆曲线， G为基点， n为点G的阶， h 是椭圆曲线上所有点的个数m与n相除的整数部分）
      这几个参量取值的选择，直接影响了加密的安全性。参量值一般要求满足以下几个条件：
   （1）p 当然越大越安全，但越大，计算速度会变慢，200位左右可以满足一般安全要求；
   （2）p≠n×h； 3、p^t≠1 (mod n)，1≤t<20； 4、4a³+27b²≠0 (mod p)； 5、n 为素数； 6、h≤4。   2、用椭圆曲线构造密码体制       描述一个利用椭圆曲线进行加密通信的过程：        （1）用户A选定一条椭圆曲线Ep(a,b)，并取椭圆曲线上一点，作为基点G,选择一个私有密钥k，并生成公开密钥K=kG。
     （2）用户A将Ep(a,b)和点K，G传给用户B。
     （3）用户B接到信息后 ，将待传输的明文编码到Ep(a,b)上一点M^[6]，并产生一个随机整数r（r<n）,计算点C₁=M+rK;C₂=rG。
     （4）用户B将C₁、C₂传给用户A。
     （5）用户A接到信息后，计算C₁-kC₂，结果就是点M。因为 C₁-kC₂=M+rK-k(rG)=M+rK-r(kG)=M 再对点M进行解码就可以得到明文。
      在这个加密通信中，如果有一个入侵者H ，他只能看到Ep(a,b)、K、G、C₁、C₂ 而通过K、G 求k 或通过C₂、G求r 都是相对困难的。因此，H无法得到A、B间传送的明文信息。 
        

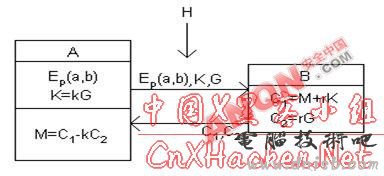
图2 基于椭圆曲线的密码体制       3、基于椭圆曲线的数字签名方案       数字签名是用来保证信息传输过程中信息的完整性和提供信息发送者的身份认证和不可抵赖性.使用公开密钥算法是实现数字签名的主要技术.公开密钥算法的运算速度比较慢,因此可使用安全的单向散列函数对要签名的信息进行摘要处理,减少使用公开密钥算法的运算量.        下面给出的ECC数字签名方案是基于IEEE P1363标准草案给出的,具体过程为:        算法描述:假设用户A向用户B发送信息M并进行签名.        用户A方的过程:   （1）确定安全Hash函数,定义椭圆曲线也就是确定参数 T=(p,a,b,G,n,h)； （2）建立密钥对(d,Q),其中d是私钥,Q=dG是公钥； （3）向用户B发送Hash函数,椭圆曲线参数和公钥Q; （4）进行签名操作:1）选择一个随机或伪随机数K,1<K<n-1;2）计算KG=(X₁,Y₁),r=X₁ mod n,若r=0,则转①;③计算K^-1mod n,e=SHA(M),其中M是明文;④计算S= K^-1(e+dr)(mod n),若S=0则转①;⑤输出签名(r, S);         用户B收到A法过来的明文M和签名(r, S)后,做以下操作:         ① 验证r和S是(1,n^-1)间的整数②计算E=SHA(M),W=S^-1(mod n) ③U₁=EW(mod n),U₂=rW(mod n) ④计算X＝U₁G + U₂Q=(X₁,Y₁),令V= X₁ mod n⑤如果r=V则接受签名. 　       随着我国推进电子政务力度的加强,电子政务将会得到很大的发展,同时它的安全问题就会暴露出来.通过密码体制来达到传输安全是一贯的做法.而椭圆曲线密码体制与其它公钥密码体制相比,有很大的优越性,从而它的应用前景将会更加广阔。（作者单位　陕西师范大学　西安电子科技大学）   参考文献  [1] IEEE P1363 :Standard for Public key cryptography working draft 1998,08 [2] Schoof R. Elliptic Curve over finite fields and computation of square Roots mod p. mathm.  of  computation 1985 [3] 彭建芬 计算椭圆曲线中的KP算法 通信技术 2